Max Flow's Cold War Origin

This is a repost of my twitter thread, which has more pictures.

I have been working on network flows which led me down a rabbit hole tracing the history of the maximum flow problem. The original formulation wasn’t declassified until 1999––almost 45 years after it was written!

We typically learn about the max flow problem and associated algorithm in the context of Ford and Fulkerson’s work, but they mention a T. Harris in their paper. Who was this guy? Where did this “rail network” motivation come from?

RAND and rail network capacities

During the Cold War, the U.S. Air Force tasked T.E. Harris and General F. S. Ross with studying Soviet railway network. The goal: determine the Soviet Union’s ability to move around soldiers and supplies. They formulated this problem as finding a maximum flow over a graph. ^[1]

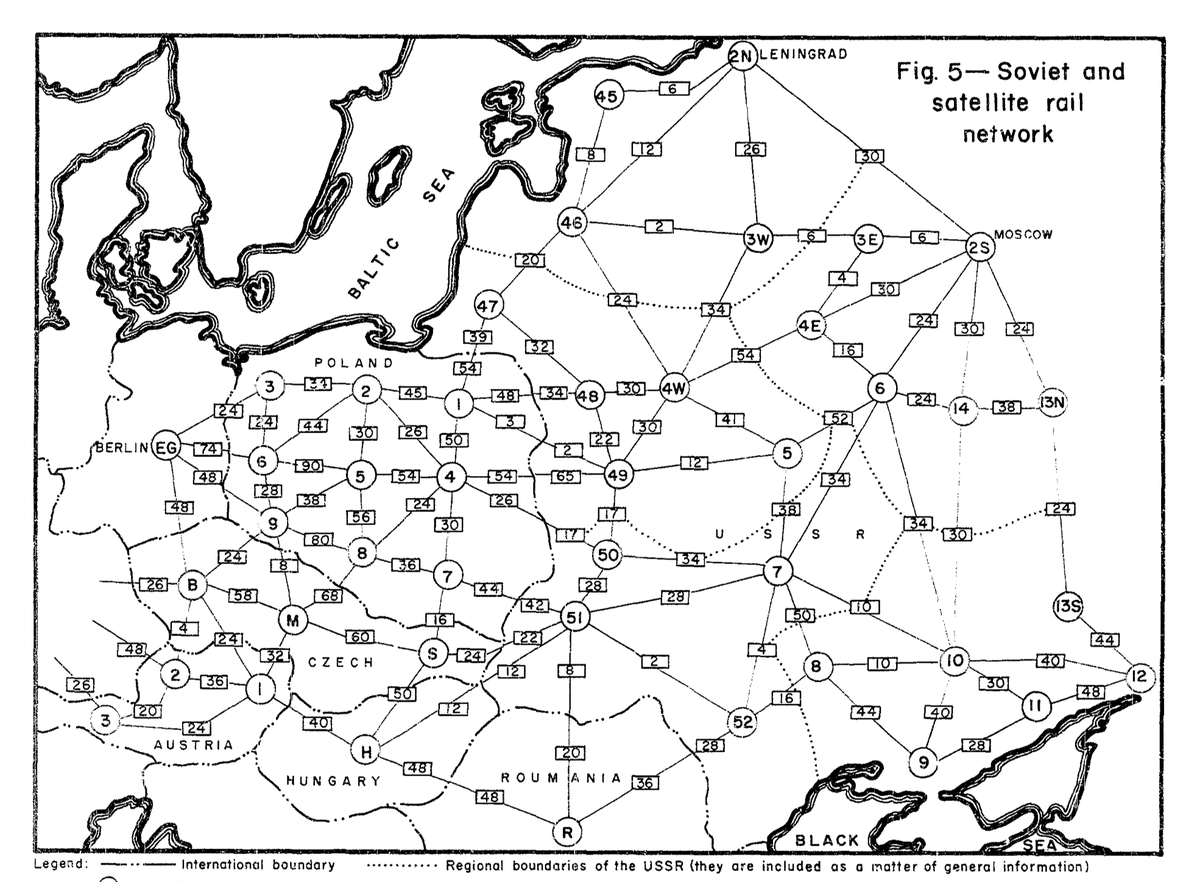
Stone age linear programming

While this problem was known to be a linear program at the time, the simplex method was too computationally expensive for practical networks. ^[2] They needed a specialized algorithm that took advantage of the network structure. In their words:

The applicability of the method proposed in this paper depends largely on the use of suitable working schemes.

They used the (heuristic) 'flooding technique' from Boldyreff: greedily push as much flow as possible through the network. This technique naturally found a bottleneck, suggesting a 'minimum cut' (later, the famous max-flow min-cut theorem was proved).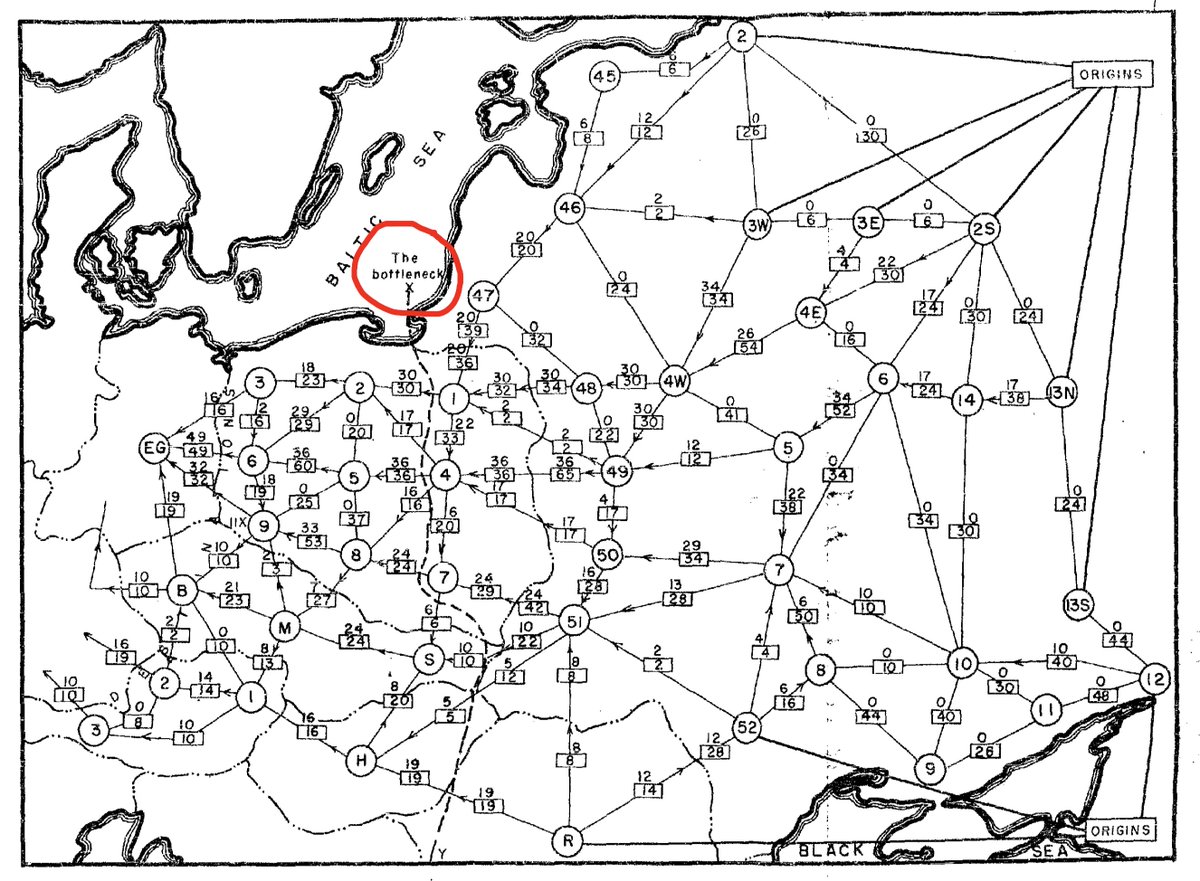

These bottlenecks (a minimal set of critical rail lines) were, of course, of interest to the US Air Force. They summarize:

Air power is an effective means of interdicting an enemy's rail system, and such usage is a logical and important mission for this Arm.

Fortunately, we never saw this application play out in practice, but the max flow problem and its generalizations now show up all over the place–-from computer networks to 2010's era burrito delivery.

Acknowledgements

This history was brought to my attention by Alexander Schrijver, who requested the declassification of the report and wrote a great historical account of these problems: On the History of the Transportation and Maximum‑Flow Problems.

Footnotes